Batch 3 - Class 124 - How do Ants find Food
Pre-Class Problem:
(Dudeney - 230) Here is a pretty little puzzle that only requires twelve pennies or counters. Arrange them in a circle, as shown in the illustration. Now take up one penny at a time and, passing it over two pennies, place it on the third penny. Then take up another single penny and do the same thing, and so on, until, in six such moves, you have the coins in six pairs in the positions 1, 2, 3, 4, 5, 6. You can move in either direction round the circle at every play, and it does not matter whether the two jumped over are separate or a pair.
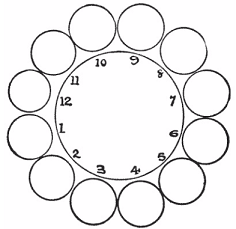
- Answer: 12->3, 7->4, 10->6, 8->1, 9->5, 11->2
- What if we wanted them to jump two stacks of pennies, regardless of number of pennies in that stack?
- Answer: 10->1, 9->6, 11->2, 8->5, 12->3, 7->4
Attendance: Smiti, Muskaan, Tishyaa, Liza, Ahana, Zorawar
Class Notes:
If two immortal people were placed on opposite sides of an uninhabited Earthlike planet, how long would it take then to find each other? 100,000 years? 1,000,000 years? 100,000,000 years?
- What approach would you follow?
- What is a good strategy?
- What is you had a chance to decide strategy in advance? Simple - just meet at the north pole?
- What if you don't have a chance to decide strategy in advance?Roam about in areas where you can see a long distance - desert rather than forests?Walk along lines - like beaches - reduces the span of search from area to line?Walk clockwise? What if the other person was also moving clockwise?May be walk clockwise a full circle, then flip a coin and basis that switch direction or not?Walk randomly?
- How do ants find food?
- How would you find food if you didn't know where it was?
- Well, send a scouting party, which randomly searches for food, and when they find it, they come back to the nest and tell everyoneHow do you know how to get back to the nest?How do you know how to get back to the food?Well, leave "pheromones" along both ways - while going out leave pheromones to mark way back home. If you find food, then on your way back, leave even more pheromones!
- What should other scouts do?If they find a trail with "even more pheromones", they should start following itWhat if they reach the nest empty-jawed instead of the food? - well, turn aroundWhat if they reach the food? - well pick some food and turn around on same trail
- How do we reinforce the shortest path to foodSince each time someone follows the path, they leave pheromones, the shorter paths will start to have more and more pheromones, and hence will get stronger
- What would happen if we had two pheromones - one "home pheromone" and one "food pheromone" - how would that make the search more efficient?
- What does this have to do with finding random people?
- Well, walk randomly and leave pheromones - i.e. marker stones. Better, we can even leave the direction and date!
- If you find a more recent trail than you have found before, follow the new one
- Hey, the person in front needs to give time for the other person to catch up. So if you are on your own fresh trail, then walk one day, rest three days.
- So how much time does it take?
- Answer: If they are walking around at random for 12 hours a day, and had to get within a kilometer to see each other, then it takes them 3000 years. Go figure!
Homework
(Dudeney - 284) In the illustration we have a somewhat curious target designed by an eccentric sharpshooter. His idea was that in order to score you must hit four circles in as many shots so that those four shots shall form a square. It will be seen by the results recorded on the target that two attempts have been successful. The first man hit the four circles at the top of the cross, and thus formed his square. The second man intended to hit the four in the bottom arm, but his second shot, on the left, went too high. This compelled him to complete his four in a different way than he intended. It will thus be seen that though it is immaterial which circle you hit at the first shot, the second shot may commit you to a definite procedure if you are to get your square. Now, the puzzle is to say in just how many different ways it is possible to form a square on the target with four shots.
.png)
- Answer: Twenty-one different squares may be selected. Of these nine will be of the size shown by the four A's in the diagram, four of the size shown by the B's, four of the size shown by the C's, two of the size shown by the D's, and two of the size indicated by the upper single A, the upper single E, the lower single C, and the EB. It is an interesting fact that you cannot form any one of these twenty-one squares without using at least one of the six circles marked E.
.png)
References:
https://ia902701.us.archive.org/4/items/AmusementsInMathematicspdf/AmusementsInMathematics.pdf - Dudeney
What If?, by Randall Munroe